(R) TURF Analysis (SPSS)

Unless you possess a background in advertising, you probably have never heard of TURF Analysis. TURF is an acronym for “Total Unduplicated Reach and Frequency”. In contrast to many of the methods previously featured on this site, TURF Analysis is rather intuitive and easily derived.

What this method seeks to accomplish, is the generation of a frequency output which demonstrates the best possible scenario, in which, the greatest number of individuals are positively impacted.

The initial data input exists as a data frame which consists of response data gathered from a questionnaire. Individuals who were surveyed were asked to provide a binary response (Yes/No) as it pertains to preference related to a series of items or scenarios. For example, you could imagine the scenario in which restaurant patrons were surveyed as it pertains to menu items which they would consider ordering.

Example (R):

We will utilize the sample data frame “turf_ex_data”, which is included within the R package “turfR”.

# With the R package: “turfR” downloaded and enabled #

The data set resembles the following initially

respid – This column contains the variable id for each individual respondent.

wgt – This is the assumed weight of each respondent. We will be ignoring this data for our example scenario.

Item_1 – Item_10 – This series of variables contains the binary response data as it pertains to the individual’s preference related to the represented item.

Since weight is required for the TURF function included within the “turfR” package, we will modify the data frame so that this variable is nullified for our example purposes. This is achieved by running the following code which creates a copy of the initial data frame, and then subsequently sets the weight values of the duplicate data frame variables to “1”.

turftest <- turf_ex_data

turftest$wgt <- 1

How we decide to proceed depends on what we are seeking to achieve with our research. If we desired to discover the three most popular items listed amongst the total set of ten items, we would run the following code:

# (dataframename, totalnumberofcolumnselections, outputcombination) #

exampleoutput <- turf(turftest, 10, 3)

exampleoutput

In this case, the following output would be produced:

> exampleoutput <- turf(turftest, 10, 3)
3 of 10: 0.02860188 sec
total time elapsed: 0.02960205 sec
> exampleoutput
$`turf`
$`turf`[[1]]
combo              rchX          frqX     1 2 3 4 5 6 7 8 9 10
1      120      0.9944444 2.4277778 0 0 0 0 0 0 0 1 1 1
2      119      0.9944444 2.3888889 0 0 0 0 0 0 1 0 1 1
3      110      0.9944444 2.1666667 0 0 0 0 1 0 0 0 1 1
4      116      0.9888889 2.3333333 0 0 0 0 0 1 0 0 1 1
5      115      0.9888889 2.2611111 0 0 0 0 0 1 0 1 0 1
6      117      0.9888889 2.2333333 0 0 0 0 0 0 1 1 1 0
7      113      0.9888889 2.2222222 0 0 0 0 0 1 1 0 0 1
8      109      0.9888889 2.0944444 0 0 0 0 1 0 0 1 0 1
9      85        0.9888889 2.0500000 0 0 1 0 0 0 0 0 1 1
10    99        0.9888889 1.9944444 0 0 0 1 0 0 0 1 0 1

What this output is illustrating, is that there is tie amongst the combination of the three most popular items. This is evident in combos: 120, 119, 110 – all of which indicate a tie in percentage of the sample reached (99.44%). If you were a restaurant owner who conducted this study in order to provide guidance as you underwent the process of reducing you menu to only three items, your next step as it relates to this study, would be to consider which sum of items within the three combos provides the greatest net income to your establishment.

In a different scenario, we may want to discover the two most popular selections amongst variables 1-5. To achieve the desired output related to such, we would have to run the following code:

turftest <- turf_ex_data[, -c(8:12)]
turftest$wgt <- 1
exampleoutput <- turf(turftest, 5, 3)
exampleoutput

Which produces the following output:

> exampleoutput <- turf(turftest, 5, 3)
3 of 5: 0 sec
total time elapsed: 0.01659989 sec
> exampleoutput
$`turf`
$`turf`[[1]]
combo     rchX       frqX     1 2 3 4 5
1 10 0.8333333 1.2000000 0 0 1 1 1
2 9 0.7611111 1.0222222 0 1 0 1 1
3 8 0.7388889 1.0055556 0 1 1 0 1
4 6 0.7166667 0.9388889 1 0 0 1 1
5 5 0.7000000 0.9222222 1 0 1 0 1
6 7 0.7000000 0.9055556 0 1 1 1 0
7 4 0.6555556 0.8222222 1 0 1 1 0
8 3 0.6166667 0.7444444 1 1 0 0 1
9 2 0.5388889 0.6444444 1 1 0 1 0
10 1 0.5166667 0.6277778 1 1 1 0 0

$call
turf(data = turftest, n = 5, k = 3)

For the function “turf” to function correctly, the data frame must be structured in the following manner:

id | weight | item(s)

It is also important to note, that errors will be returned and the function will not proceed if the number of item columns within the function, do not exactly equal the number of item columns within the data frame.

Example (SPSS):

To perform this example, you will need to export the “turf_ex_data” data frame as a file encoded within the .csv format. This can be achieved by modifying the code below:

write.table(turf_ex_data, file = "C:/Users/Desktop/turf_ex_data.csv", sep = ",", col.names = NA, row.names = TRUE)

Once this file has been exported to the desktop, you can proceed with importing it into the SPSS platform.

To begin, you must first select “Analyze” from the upper left drop down menu, then select “Descriptive Statistics”, followed by “TURF Analysis”.

This should present the following interface:

Utilizing the top center arrow, designate all of the item variables as the “Variables to Analyze”. Next, set “Maximum Variable Combinations” to equal “10”. After this is complete, designate “Number of Combinations to Display” to equal “3”. Finally, remove the check mark adjacent to the box labeled, “Reach and frequency plot”. Once all of this is complete, click “OK”.

This should generate the following output:

Which is the output which you initially requested. However, SPSS also provides additional output which is also interesting.

(Each item individually)

(Additional combinations)

You may also notice that SPSS provides a different output cell structure as compared to the unstructured and simplistic output of the R console.

Reach – Refers to the number of individuals satisfied, or reached*, within the current combination.

Pct of Cases – Percent of individuals within the reach category as compared to the entire sample size (x/180).

Frequency – The sum of the positive responses measured for each item within the categorical set**.

Pct of Response – The total frequency of the response (number of times individuals answered “1” to the item), divided by the total frequency measuring the positive responses pertaining to all items (number of times individuals answered “1” to any item including the response item).

*- Individuals who chose “yes” as it relates to an item variable within the combination.

**- Example: 132 positive responses for item 8, 145 positive responses for item 9, 160 positive responses for item 10. 132 + 145 + 160 = 437 (Frequency).

That’s all for now! Stay enthused, Data Heads!

(R) Survival Analysis - Kaplan-Meier and Cox Models (SPSS)

Survival Analysis is a statistical methodology which measures the probability of an event occurring within a group over a period of time.

If you have a decent understanding of the linear regression concept, understanding the output generated by the survival analysis model is fairly simple.

We will demonstrate the methodology of survival analysis through various examples. The data set which will be utilized for the following demonstrations is found within the R “survival” package.

Example: Survival Analysis - Kaplan-Meier Model (R)

# With the R package: “survival” downloaded and enabled #

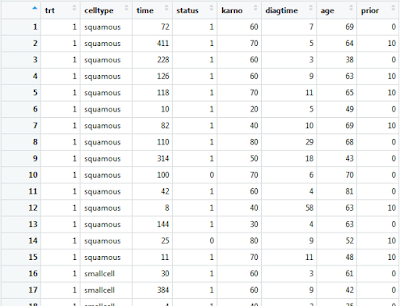
The R “survival” package comes with the “veteran” data frame embedded within its composition. With the “survival” package enabled, the “veteran” data frame can be called with the command: “veteran”.

If you wish to view this data frame within the R-Studio graphical user interface, you must first assign it to a native data frame variable.

vet1 <- veteran

Double clicking on this data frame variable within the environment frame of R-Studio will present you with the following:

To begin performing a Kaplan-Meier survival analysis within the R platform, you must utilize the following line of code:

kmsurvival <- survfit(Surv(time, status) ~ 1, data=vet1)

This code will indicate to R that a Kaplan-Meier survival analysis should be embarked upon. The “time” variable is indicating the time status, and the “status” variable is indicating censor status (1 = Non-Censored, 0 = Censored). In the case of this particular model, both data frame variables are named exactly what the variable type implies. Please be aware that data frames variables are not always perfectly assigned in this manner.

To view the model output, we will invoke the following function:

summary(kmsurvival)

Which produces the following output:

> summary(kmsurvival)
Call: survfit(formula = Surv(time, status) ~ 1, data = vet1)

time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 137 2 0.985 0.01025 0.96552 1.0000
2 135 1 0.978 0.01250 0.95390 1.0000
3 134 1 0.971 0.01438 0.94302 0.9994
4 133 1 0.964 0.01602 0.93261 0.9954
7 132 3 0.942 0.02003 0.90315 0.9817
8 129 4 0.912 0.02415 0.86628 0.9610
10 125 2 0.898 0.02588 0.84850 0.9500
11 123 1 0.891 0.02668 0.83973 0.9444
12 122 2 0.876 0.02817 0.82241 0.9329
13 120 2 0.861 0.02953 0.80534 0.9212
15 118 2 0.847 0.03078 0.78849 0.9092
16 116 1 0.839 0.03137 0.78013 0.9032
18 115 3 0.818 0.03300 0.75533 0.8848
19 112 2 0.803 0.03399 0.73900 0.8724
20 110 2 0.788 0.03490 0.72280 0.8598

The output itself is much greater in length but I have only included the first 20 observations.

In discussing each unique aspect of the output:

time – This variable illustrates the categorical point in time when a measurement was taken.

n.risk – This variable represents the number of individuals remaining within the initial group of measured individuals.

n.event – This variable represents the total number of individuals who were removed from the remaining group of individuals at the measured point in time.

survival – The probability of any individual within the initial group being a remaining member of the group at this present point in time.

Typically, with survival analysis, the application of the methodology is demonstrated through examples pertaining to drug trials. We could imagine, a scenario which involves patients undergoing treatment for some ailment until their symptoms subside. This gradual diminishment of initial individuals involved in the study is illustrated in the output below:

As the categorical measurement of time progresses (63 – 72), the n.risk figure decreases (72 – 71), this is demonstrated by the number of individuals who no longer meet the initial groups classification (n.event = 1). However, how can we explain the phenomenon in which more individuals leave the study than are not accounted for? This is the case for the numerical values encircled in blue.

You may recall earlier, that we specified for the variable “status” within our “survfit” function. What does this variable connotate within the context of our original data frame?

Censoring

As it pertains to survival analysis, the term “censoring” refers to the event in which an individual leaves the original group without the measured even occurring. For example, in the case of a study, this could occur if an individual stops corresponding with the researchers. Or for a more morbid example, if an individual passes away as a result of circumstance un-related to the study.

In either situation, this non-event loss of individuals from the initial group will be connotated by a cross marking on the graphed output. These individuals are considered “censored” individuals.

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled #

autoplot(kmsurvival)

Which produces the following output:

The center solid line represents the survival probability of the model, the outside grey area represents the 5% and 95% confidence intervals. The cross markings on the solid central line indicate an instance when censoring took place.

Example: Survival Analysis - Kaplan-Meier Model (R)

We will now produce a model which contains the same parameters of the previous model. The graphical output created as a result of such is the product of two separate sets of analysis, each set specifying a pre-determined condition. Each conditional scenario will be illustrated within the model output as separate solid lines.

To achieve this desired results, we must run the following lines of code:

# With the R package: “survival” downloaded and enabled #

# In this case, our factor is “trt” #

kmsurvival <- survfit(Surv(time, status) ~ trt, data=vet1)

To view the model output, we will invoke the following function:

summary(kmsurvival)

Which produces the following output:

Call: survfit(formula = Surv(time, status) ~ trt, data = vet1)
trt=1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
3 69 1 0.9855 0.0144 0.95771 1.000
4 68 1 0.9710 0.0202 0.93223 1.000
7 67 1 0.9565 0.0246 0.90959 1.000
8 66 2 0.9275 0.0312 0.86834 0.991
10 64 2 0.8986 0.0363 0.83006 0.973
11 62 1 0.8841 0.0385 0.81165 0.963
12 61 2 0.8551 0.0424 0.77592 0.942
13 59 1 0.8406 0.0441 0.75849 0.932
16 58 1 0.8261 0.0456 0.74132 0.921
18 57 2 0.7971 0.0484 0.70764 0.898
20 55 1 0.7826 0.0497 0.69109 0.886

(and)

trt=2
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 68 2 0.9706 0.0205 0.93125 1.000
2 66 1 0.9559 0.0249 0.90830 1.000
7 65 2 0.9265 0.0317 0.86647 0.991
8 63 2 0.8971 0.0369 0.82766 0.972
13 61 1 0.8824 0.0391 0.80900 0.962
15 60 2 0.8529 0.0429 0.77278 0.941
18 58 1 0.8382 0.0447 0.75513 0.930
19 57 2 0.8088 0.0477 0.72056 0.908
20 55 1 0.7941 0.0490 0.70360 0.896

Again, I shortened the output to conserve space. However, as is evident within the portions of output, each particular condition is illustrated above the conditional output type. (trt = 1, trt = 2)

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled # 

autoplot(kmsurvival)

Which produces the following output:

Notice that in this case, two separate confidence interval areas have been produced, each pair existing as an aspect of the solid line in which it engulfs.

Example: Survival Analysis – Cox Proportional Hazard Model (R)

The Cox Proportional Hazard Model, like the Kaplan-Meier Model, is also a survival analysis methodology. The Cox Model is more complicated in its composition as it allows for the inclusion of additional variables. The inclusion of these additional variables, if correctly integrated, can yield a more descriptive model. However, as a consequence of the model’s complication, the additional aspects which provide positive differentiation, can also lead to the increased probability of user error.

To create a Cox Proportional Hazard Model, we will utilize the following lines of code:

# With the R package: “survival” downloaded and enabled #

coxsurvival <- coxph(Surv(time, status) ~ trt + karno + diagtime + age + prior , data=vet1)

summary(coxsurvival)

This produces the output:

Call:
coxph(formula = Surv(time, status) ~ trt + karno + diagtime +
age + prior, data = vet1)

n= 137, number of events= 128

coef exp(coef) se(coef) z Pr(>|z|)
trt 0.193053 1.212947 0.186446 1.035 0.300
karno -0.034084 0.966490 0.005341 -6.381 1.76e-10 ***
diagtime 0.001723 1.001725 0.009003 0.191 0.848
age -0.003883 0.996125 0.009247 -0.420 0.675
prior -0.007764 0.992266 0.022152 -0.350 0.726
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

exp(coef) exp(-coef) lower .95 upper .95
trt 1.2129 0.8244 0.8417 1.7480
karno 0.9665 1.0347 0.9564 0.9767
diagtime 1.0017 0.9983 0.9842 1.0196
age 0.9961 1.0039 0.9782 1.0143
prior 0.9923 1.0078 0.9501 1.0363

Concordance= 0.714 (se = 0.03 )
Rsquare= 0.271 (max possible= 0.999 )
Likelihood ratio test= 43.27 on 5 df, p=3.259e-08
Wald test = 44.88 on 5 df, p=1.537e-08
Score (logrank) test = 47.39 on 5 df, p=4.734e-09

Primarily, when analyzing the model summary data, we should concern ourselves with the portions of the output which I have highlighted in bold. The initial portion of the output provides values, which are found within the rightmost column, which indicate the strength of each variable as it impacts the overall outcome of the model (Pr(>|z|).

The p-value of the Wald Test (1.537e-08 < .05), indicates that the model is significant. While the r-squared value (.271), indicates that the model is not a particularly good fit as it pertains to the existing data points.

To create a graphical output for our example model, we would utilize the following code:

# With the R packages: “ggplot2”, and "ggfortify" downloaded and enabled # 

coxsurvival <- survfit(coxsurvival)

autoplot(coxsurvival)

Which produces the following output:

Example: Survival Analysis – Cox Proportional Hazard Model with Time Dependent Co-Variates (R) 

There may be instances in which you will encounter survival data which contains time dependent co-variates. What this translates to, in simpler terms, is that the data which you are preparing to analyze contains variables which are dependent on time duration.

The data in these scenarios is typically organized in a manner similar to data presented below:

As is demonstrated within the data set, individuals have been surveyed multiple times. This method has been utilized to account for the variables “symphtomA” and “symphtomB”, which typically occur as a result of the treatment methods occurring over set intervals of time.

It may appear that the time intervals are overlapping in the above example, however, this is not the case. When setting up data for analysis in the manner, it must be structured similarly, with duration aspects appearing to overlap. The lack of ambivalence is due to measurements being taken at the end of each interval. So, in the case of ID:3, measurements were taken at day 50, day 100, day 150, day 200, and day 250.

To begin performing a Cox Proportional Hazard Model with Time Dependent Co-Variates within the R platform, you must utilize the following lines of code:

(I am aware that this sample data, model, and graphical output are equally awful. However, I could not find a worthwhile example to demonstrate, and making data sets from scratch which contain decent representational entries is extremely difficult. The .csv file utilized to create this example can be found at the end of the article.)

coxsurvival1 <- coxph(Surv(time1, time2, status) ~ trt + karno + diagtime + age + symphtomA + symphtomB , data=vet2)

summary(coxsurvival1)

This produces the output:

Call:
coxph(formula = Surv(time1, time2, status) ~ trt + karno + diagtime +
age + symphtomA + symphtomB, data = vet2)

n= 22, number of events= 21

coef exp(coef) se(coef) z Pr(>|z|)
trt 3.959e-16 1.000e+00 1.225e+00 0.000 1.000
karno -2.636e-17 1.000e+00 8.672e-02 0.000 1.000
diagtime -1.281e-16 1.000e+00 1.713e-01 0.000 1.000
age 2.730e-17 1.000e+00 5.009e-02 0.000 1.000
symphtomA -9.177e-16 1.000e+00 7.906e-01 0.000 1.000
symphtomB -1.985e+01 2.392e-09 1.510e+04 -0.001 0.999

exp(coef) exp(-coef) lower .95 upper .95
trt 1.000e+00 1.00e+00 0.09061 11.036
karno 1.000e+00 1.00e+00 0.84370 1.185
diagtime 1.000e+00 1.00e+00 0.71474 1.399
age 1.000e+00 1.00e+00 0.90649 1.103
symphtomA 1.000e+00 1.00e+00 0.21236 4.709
symphtomB 2.392e-09 4.18e+08 0.00000 Inf

Concordance= 1 (se = 1.594 )
Rsquare= 0.118 (max possible= 0.723 )
Likelihood ratio test= 2.77 on 6 df, p=0.8368
Wald test = 0 on 6 df, p=1
Score (logrank) test = 1.78 on 6 df, p=0.9389

To create a graphical output for our example model, we would utilize the following code:

# With the R package: “survival” downloaded and enabled #

coxsurvival1 <- survfit(coxsurvival1)

autoplot(coxsurvival1)

Which produces the following output:

Example: Survival Analysis - Kaplan-Meier Model (SPSS)

To re-create this example, you must first export the “veteran” data set to a .csv file, and then subsequently import it into the SPSS platform.

The result of such should resemble the following:

To begin, you must first select “Analyze” from the upper left drop down menu, then select “Survival”, followed by “Kaplan-Meier”.

This should present the following interface:

Utilizing the top center arrow, designate the variable “time” as the “Time” entry. Then, utilize the second topmost arrow to designate the variable “status” as the “Status” entry.

Once this step has been completed, click on the box labeled “Define Event”.

From the sub-menu generated, input “1” as the “Single value”, then click “Continue”.

Next, click on the menu box labeled “Options”.

This should cause the following menu to populate:

Be sure to check the boxes to the left of the “Mean and medial survival” and “Survival” options.

Once this is completed, click “Continue”, and then click “OK”.

This s will generate the following output:

The model parameters can be modified in the initial menu to produce an output which is differentiated by a factor variable.

This modification would produce the output:

Example: Survival Analysis – Cox Proportional Hazard Model (SPSS)

We will be utilizing the same data set which analyzed in the previous example:

To begin, you must first select “Analyze” from the upper left drop down menu, then select “Survival”, followed by “Cox Regression”.

This should present the following interface:

Utilizing the top center arrow, designate the variable “time” as the “Time” entry. Then, utilize the second topmost arrow to designate the variable “status” as the “status” entry. Finally, utilize the middle center arrow to designate the variables “trt”, “karno”, “diagtime”, “age”, and “prior” as “Covariates”.

Once this step has been completed, click on the box labeled “Define Event”.

From the sub-menu generated, input “1” as the “Single value”, then click “Continue”.

Next, click on the menu option labeled “Plots”.

Within this interface, select the box to the left of the option labeled “Survival”, then click “Continue”.

Once this has been completed click “OK”.

This should produce the following output:

Survival Analysis – Cox Proportional Hazard Model Example File (.csv)

id,trt,celltype,time1,time2,status,karno,diagtime,age,prior,symphtomA,symphtomB
1,1,squamous,0,50,1,60,7,69,0,0,0
1,1,squamous,50,100,1,60,7,69,0,1,0
2,1,squamous,0,50,1,70,5,64,10,1,0
2,1,squamous,50,100,1,70,5,64,10,0,0
2,1,squamous,100,150,1,70,5,64,10,1,0
2,1,squamous,150,200,1,70,5,64,10,1,0
2,1,squamous,200,250,1,70,5,64,10,1,0
2,1,squamous,250,300,1,70,5,64,10,1,0
2,1,squamous,300,350,1,70,5,64,10,1,1
2,1,squamous,350,400,1,70,5,64,10,1,1
2,1,squamous,400,450,1,70,5,64,10,1,1
3,2,squamous,0,50,1,60,3,38,0,0,0
3,2,squamous,50,100,1,60,3,38,0,1,0
3,2,squamous,100,150,1,60,3,38,0,1,0
3,2,squamous,150,200,1,60,3,38,0,1,0
3,2,squamous,200,250,1,60,3,38,0,1,0
4,2,squamous,0,50,1,60,9,63,10,0,0
4,2,squamous,50,100,1,60,9,63,10,1,0
4,2,squamous,100,150,1,60,9,63,10,1,0
5,1,squamous,0,50,1,70,11,65,10,0,0
5,1,squamous,50,100,1,70,11,65,10,0,0
5,1,squamous,100,150,0,70,11,65,10,0,1

That’s all for now, Data Heads! Stay tuned for more informative content!

(R) Odds Ratio, Relative Risk and Cohen’s Kappa

In this article, we will be discussing Odds Ratio, Relative Risk, The Cohen's Kappa Statistic, and their relation to data contained within contingency tables. Additionally, I will be sharing some code which I have created within the R platform which will simplify the process of generating these figures.

Example:

We will address the typical scenario which involves smoking as it relates to cancer diagnosis.

We will create three data vectors. Each data vector will contain data collected from a single individual. The first data vector will contain an identification variable pertaining to individual. The next data vector will contain a binary variable which identifies smokers and non-smokers alike. The final variable will indicate which individuals are afflicted with cancer.

# Create Data Vectors #

id <- c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)

smoker <- c(0,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,0,0,0,0)

cancer <- c(0,0,1,1,0,0,1,1,1,1,1,1,0,0,1,1,1,0,0,0)

smokerscancer <- data.frame(id, smoker, cancer)

This data frame now must be transformed into a matrix before it can be analyzed.

This can be achieved through the following code:

# Organize Data into Contingency Table #

x <- smokerscancer$smoker

y <- smokerscancer$cancer

cases <- data.frame(x,y)

cases$y <- c(ifelse(cases$y == 1, 'aTrue', 'bFalse'))

cases$x <- c(ifelse(cases$x == 1, 'aTrue', 'bFalse'))

cases <- cases[complete.cases(cases), ]

ctable <- table(cases)

# Apply Chi-Squared Test of Independence #

chisq.test(ctable)

Which produces the following output:

Pearson's Chi-squared test with Yates' continuity correction

data: ctable
X-squared = 3.2323, df = 1, p-value = 0.0722

For more information as how to interpret Chi-squared output, please consult this article.

The following code produces additional output, along with the original contingency table:

# Produce Odds Ratio / Relative Risk Outputs #

totala <- ctable[1,1] + ctable[1,2]
totalb <- ctable[2,1] + ctable[2,2]
percent1 <- (ctable[1,1] / totala) * 100
percent2 <- (ctable[1,2] / totala) * 100
percent3 <- (ctable[2,1] / totalb) * 100
percent4 <- (ctable[2,2] / totalb) * 100
totalc <- ctable[1,2] + ctable[2,2]
totald <- ctable[1,1] + ctable[2,1]
totale <- totalc + totald
rowtotala <-totald/(totalc + totald) * 100
rowtotalb <-totalc/(totalc + totald) * 100
rowtotalc <- (rowtotala + rowtotalb)

keycol <- c("Count", "(%)", "Count", "(%)", "SumCount", "(%)")
col1 <- c(ctable[1,1], percent1, ctable[2,1], percent3, totald, rowtotala)
col2 <- c(ctable[1,2], percent2, ctable[2,2], percent4, totalc, rowtotalb)
rowtotals <- c((ctable[1,1] + ctable[1,2]), (percent1 + percent2), (ctable[2,1] + ctable[2,2]), (percent3 + percent4), (totalc + totald), rowtotalc)

data <- data.frame(keycol, col1, col2, rowtotals)

vala <- percent3 / percent1
valb <- percent4 / percent2
valab <- valb/vala

num <- (ctable[1,1]) / (ctable[1,1] + ctable[1,2])
den <- (ctable[2,1]) / (ctable[2,1] + ctable[2,2])
relrisk <- num/den

ctable

data

valab # (Odds Ratio) col1 (%/%) / col2 (%/%) #

relrisk # Relative Risk = TRUE col1 (%/%) #

Which produces the following output:

        y
x           aTrue bFalse
aTrue       8        2
bFals      3        7

       keycol    col1    col2    rowtotals
1      Count     8        2          10
2      (%)       80      20       100
3      Count    3        7         10
4      (%)     30      70        100
5      SumCount 11 9         20
6     (%)     55      45 1      00

valab # (Odds Ratio) col1 (%/%) / col2 (%/%) #

[1] 9.333333

relrisk # Relative Risk = TRUE col1 (%/%) #

[1] 2.666667

This output was created to resemble the table generated by SPSS as it pertains to chi-squared contingency data.

But how are the results within this table interpreted?

If your data is structured in the manner in which the contingency table within the example is organized, we can make the following statements.

Risk ratios indicated that the risk of the outcome variable (cancer), within the category of smokers, increased by 167 %* relative to the group of non-smokers. Or, the outcome of this event was 2.667 times more likely to occur within the smoker group.

The odds ratio indicates that the odds of finding cancer within an individual who smokes, as compared to an individual who does not smoke, is 9.333.

*= Absolute value of (1 – RR), multiplied by 100.

Cohen’s Kappa

Cohen’s Kappa, like the odds ratio and the risk ratio, is utilized to analyze the relationships of data within a contingency table. However, while the previously mentioned methods are universally applicable, Cohen’s Kappa can only be applied to contingency tables which measure categorical ratings.

Example:

Two film critics are rating a series of 20 movies. Each critic can either vote “Yes”, as an indication that he enjoyed the film, or “No”, as an indication that he did not enjoy the film. The results were recorded within a binary format.

# Create Vectors #

movieid <- c(1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20)

criticoneratings <- c(0,0,0,1,1,0,0,1,1,1,1,1,0,1,1,1,0,0,0,0)

critictworatings <- c(0,0,1,1,0,0,1,1,1,1,1,1,0,0,1,1,1,0,0,0)

movieratings <- data.frame(movieid, criticoneratings, critictworatings)

With this information, we wish to measure the level of agreement between the two raters. One of the main ways in which this technique differs from traditional probabilistic methodologies, is that this particular technique accounts for chance agreement.

Now that we have our data values correctly input, we can proceed with the analysis.

# Organize Data into Contingency Table #

x <- movieratings$criticoneratings

y <- movieratings$critictworatings

cases <- data.frame(x,y)

cases$y <- c(ifelse(cases$y == 1, 'aTrue', 'bFalse'))

cases$x <- c(ifelse(cases$x == 1, 'aTrue', 'bFalse'))

cases <- cases[complete.cases(cases), ]

ctable <- table(cases)

# With the “psych” package downloaded and enabled #

cohen.kappa(ctable,alpha=.05)

This produces the output:

Call: cohen.kappa1(x = x, w = w, n.obs = n.obs, alpha = alpha, levels = levels)

Cohen Kappa and Weighted Kappa correlation coefficients and confidence boundaries
             lower estimate upper
unweighted kappa    0.12      0.5    0.88
weighted kappa        0.12      0.5    0.88

Number of subjects = 20

I have bolded the kappa statistic (.5) contained within the output.

Opinion as to how to interpret the kappa statistic varies. Written below are the recorded opinions of professional analysts pertaining to such:

“Landis and Koch, characterized values < 0 as indicating no agreement, and 0-0.20 as slight, 0.21-0.40 as fair, 0.41-0.60 as moderate, 0.61-0.80 as substantial, and 0.81-1 as almost perfect agreement.

Fleiss's equally arbitrary guidelines characterize kappa over 0.75 as excellent, 0.40 to 0.75 as fair to good, and below 0.40 as poor. “ **

**- https://en.wikipedia.org/wiki/Cohen’s_kappa

If we were to apply this model in more gregarious manner, for the sake of spectating at the aspects of its inner workings, the following code could be applied:

# Observed Proportionate Agreement #

# Define Cell Entries #

a <- ctable[1,1]
b <- ctable[1,2]

c <- ctable[2,1]
d <- ctable[2,2]

# Observed Proportionate Agreement (p0) #

p0 <- (a + d) / (a + b + c + d)

# Expected probability that both would say yes at random (pYes) #

pyes <- ((a + b) / (a + b + c + d)) * ((a + c) / (a + b + c + d))

# Expected probability that both would say no at random (pNo) #

pno <- ((c + d) / (a + b + c + d)) * ((b + d) / (a + b + c + d))

# Overall random agreement probability is the probability that they #
# agreed on either Yes or No (pe) #

pe <- pyes + pno

# Cohen's Kappa #

K <- (p0 - pe) / (1 - pe)

That’s all for now, Data Heads! Stay tuned for more awesome articles!

(R) Repeated Measures Logistic Regression

One of the more eclectic and synthetic methods of model creation, combines the logistic regression model, with the ability to attribute for multiple re-occurring observations. I heavily advise against utilizing this method for three reasons. The first reason being, is that it is incredibly complicated. The second reason being, is that the math involved is synthetic and combines multiple concepts into a single model methodology. The final reason, is that the code utilized to aid in the model's creation, only exists within an auxillary R package, and the package itself is difficult to utilize.

However, for the sake of demonstration, here is what the code for this method might resemble:

Example:

# Create data vectors #

id <- c(1,1,1,1,1,1,2,2,2,2,2,2,3,3,3,3,3,3)

vara <- c(0,0,0,0,1,1,1,1,1,0,1,1,0,1,1,1,1,0)

varb <- c(0,0,0,0,0,0,1,1,1,0,0,1,1,1,1,0,0,0)

outcome <- c(1,1,1,1,0,0,1,1,1,1,1,0,0,0,0,0,1,1)

# With the package: “lme4”, installed and enabled #

# Apply The Repeated Measures Logistic Regression Model #

glmer(outcome~vara+varb +(1|id),family=binomial)

This creates the output:

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
Family: binomial ( logit )
Formula: outcome ~ vara + varb + (1 | id)
    AIC BIC logLik deviance df.resid
26.5032 30.0647 -9.2516 18.5032 14
Random effects:
Groups Name          Std.Dev.
id      (Intercept)       2.592
Number of obs: 18, groups: id, 3
Fixed Effects:
(Intercept)            vara           varb
        4.656          -3.757        -3.587

Which can be utilized to create a model equation.

For our example, we can assume that we have three individuals who are being tested for a binary outcome. The variables, which we believe will be impactful within this situation, are the independent variables: “vara” and “varb”. As each individual was surveyed multiple times, the repeated measures logistic regression model was utilized to attribute for this aspect of the experimental methodology.

That’s all for now data heads. Stay tuned for more useful content!

Frequency and Syntax (SPSS)

There are not many articles or videos online which specifically address the topic of “syntax”. Syntax, in this particular instance, refers to the coding language of IBM SPSS. In this article, I will briefly discuss a few useful elements which should lead to an increase in coding efficiency and a greater understanding of IBM SPSS coding syntax. Examples will primarily focus on situations which require the utilization of frequency analysis.

Creating New Syntax

To create new syntax, you must first select “File” from the upper left drop down menu, then select “New”, followed by “Syntax”.

Thus should present the following interface:

The right section of the screen serves as the console. It is this section where you will be creating your code.

I typically begin my code files with the following lines:

* Encoding: UTF-8.

* Establish working directory

cd 'C:\DirectoryPathWay\User\etc\'.

* Specify file path (make sure extension is included)

GET FILE='ExampleFile.sav'.

The first line:

cd 'C:\DirectoryPathWay\User\etc\'.

Establishes the directory from which you will be accessing your files.

The next line:

GET FILE='ExampleFile.sav'.

Is specifying the file in which the code will be referring to when performing specific functions.

You will, of course, have to modify both of the lines above so that they refer to non-fictitious items.

To run syntax from the console, you must first highlight the portions in which you wish to run, then click on the green arrow above.

If the code was correctly formatted and did not produce any errors, the output created as a product of the code’s utilization will be displayed within the output window.

The best way to generate examples of code to provide functions which you wish to utilize, is to first initiate a function from the graphical user interface. Doing such, provides the product of the function to be displayed within the output window. Along with such, is the code, which if ran as syntax, would also perform the same function.

Example (SPSS):

Let us consider the following data set:

With data labels assigned and enabled, the set resembles the following:

To perform a basic frequency analysis output, we must make the following selections. From the topmost menu bar, select “Analyze”, then select “Descriptive Statistics”, finally, select “Frequencies”.

This should cause the following menu to appear:

Utilizing the center arrow, we will designate the column “FavGenre” as our “Variable(s)”.

Once this step has been completed, click “OK”.

The following output will be produced:

Let us turn out attention to the text above the title “Frequencies”.

This output illustrates the code which was utilized as a function to generate the requested analytical output.

This code can be copied and re-utilized from the console window to re-create the output. This can be helpful when multiple queries are required, as it eliminates the tedious process of utilizing the user interface for each independent request.

For example, if you wanted to run the frequency function for multiple variables independently, you could utilize the following code:

Something that I would recommend, and this is completely optional, is the utilization of titles within your code. I find that titles being included within the output, especially when multiple functions are utilized, allows for increased readability and enhanced organization of results.

The inclusion of such would resemble:

Which would produce an output resembling:

For frequencies, if you wished to produce multiple outputs for different variables but did not want create each function independently, you could utilize the following code:

SPSS also provides a function that can be utilized to produce descriptive statistics.

To perform a descriptive frequency output, we must make the following selections. From the topmost menu bar, select “Analyze”, then select “Descriptive Statistics”, finally, select “Descriptive”.

From the menu that is generated from this series of actions, utilize the middle arrow to designate the column “FavGenre” as a “Variable(s)”.

From the sub-menu generated from selecting the “Options” box, make the following selections:

Once this has been completed, click “Continue”, and then click “OK”.

This will produce the following output:

Though it is inapplicable as it pertains to our current example, if there is a situation in which you wish to generate descriptive summary output, the following syntax can be utilized:

DESCRIPTIVES VARIABLES=Height
/STATISTICS=MEAN STDDEV MIN MAX.
If you would like to perform this function from the graphical interface, please follow the proceeding steps. From the topmost menu bar, select “Analyze”, then select “Descriptive Statistics”, finally, select “Descriptives”.



After designating the appropriate variable for analysis. A table similar to the output below should be produced.

Generating these sorts of summaries is rather simple and straightforward. However, what if we wanted to analyze data based on specific criteria?

For our example, we will assume that we only want to generate a frequency table which lists the preferred music genre for females.

The code to achieve such is as follows:

The filter temporarily disables data observations which contain a variable which matches the specified value.

If you were to run this code block independently, you would notice the following impact which it has on the data frame.

The initial lines of code perform the query itself, with the final line disabling the filter. It is important that the filter be disabled (FILTER OFF.), if additional queries are to be performed which do not specifically pertain to the parameters of the current analysis.

WARNING!!!

If you are presented with errors when applying filters, these prompts will typically stem from one of the following:

1. You are applying a filter to a data label. Remember in cases which require such filtering, to always apply the filter to the underlying numerical variable.

2. If you are applying a filter to a string variable, do not forget to include the variable within quotes (‘ ‘) .

If there is a situation in which you must apply multiple filters prior to performing analysis, the following code blocks should provide useful:

Applying multiple filters:

USE ALL.

COMPUTE filter_$=(Gender=0 AND Gender=1).

FILTER BY filter_$.

EXECUTE.

Setting a query variable to NOT EQUAL a value:

USE ALL.

COMPUTE filter_$=(Gender NE 0).

FILTER BY filter_$.

EXECUTE.

Generating query data where a variable equals one value OR another value:

USE ALL.

COMPUTE filter_$=(FavGenre = 1 OR FavGenre = 2).

FILTER BY filter_$.

EXECUTE.

That’s all for now, Data Heads! Stay subscribed for more informative content!